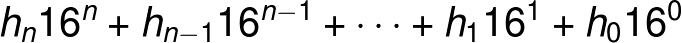Call: 480-962-4545

Home » Converting To/From Decimal

Converting To/From Decimal

By now, we know how to convert about 16-or-so values between decimal and hexadecimal. To convert bigger numbers, here are some tricks we use.

Converting Decimal to Hex

Converting from decimal to hex involves a lot of division and remainders. If you’ve pushed long division out of your brain, wiki’s always there to help you brush up.

The steps to convert a number, let’s call it N, from decimal to hex look something like this:

  1. Divide N by 16. The remainder of that division is the first (least-significant/right-most) digit of your hex number. Take the quotient (the result of the division) to the next step.
    • Note: if the remainder is 10, 11, 12, 13, 14, or 15, then that becomes the hex digit A, B, C, D, E, or F.
  2. Divide the quotient from the last step by 16 again. The remainder of this division is the second digit of your hex value (second-from-the-right). Take the quotient from this division to the next step.
  3. Divide the quotient from step 2 by 16 again. The remainder of this division is the third digit of your hex conversion. Noticing a pattern?
  4. Keep dividing your quotient from the last step by 16, and storing the remainder until the result of a division is 0. The remainder of that division is your hex value’s left-most, most-significant digit.

Decimal-to-Hex Example: Convert 61453

Enough math-speak, let’s work an example. Let’s convert 6145310 to hexadecimal:

  1. Divide 61453 by 16. The result is a quotient of 3840, and a remainder of 13. That remainder becomes our first, right-most, least-significant hex digit – D. Take 3840 to the next step.

  2. Now divide 3840 by 16. The resulting quotient is 240 with a remainder of 0. Our second hex digit is 0, and we take 240 to the next digit.

  3. Divide 240 by 16, and you’ll get 15 with another 0 remainder. Our third hex digit is 0, and take 15 to step 4.

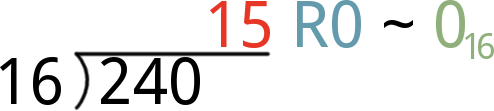
  4. Finally, divide 15 by 16. That’ll produce the 0 quotient we’ve been waiting for, with a remainder of 15. That remainder means the hex digit for this position if F.

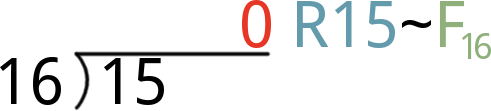
Finally, combine all four hex digits to create our hex value: 0xF00D.

Converting Hex to Decimal

There’s an ugly equation that rules over hex-to-decimal conversion:

h_{n}16^{n}+h_{n-1}16^{n-1}+\cdots +h_{1}16^{1}+h_{0}16^{0}

There are a few important elements to this equation. Each of the h factors (hn, hn-1) is a single digit of the hex value. If our hex value is 0xF00D, for example, h0 is D, h1 and h2 are 0, and h3 is F.

Powers of 16 are a critical part of hexadecimal. More-signficant digits (those towards the left side of the number) are multiplied by larger powers of 16. The least-significant digit, h0, is multiplied by 160 (1). If a hex value is four digits long, the most-significant digit is multiplied by 163, or 4096.

To convert a hexadecimal number to decimal, you need to plug in values for each of the h factors in the equation above. Then multiply each digit by its respective power of 16, and add each product up. Our step-by-step approach is:

  1. Start with the right-most digit of your hex value. Multiply it by 160, that is: multiply by 1. In other words, leave it be, but keep that value off to the side.
    • Remember to convert alphabetic hex values (A, B, C, D, E, and F) to their decimal equivalent (10, 11, 12, 13, 14, and 15).
  2. Move one digit to the left. Multiply that digit by 161 (i.e. multipy by 16). Remember that product, and keep it to the side.
  3. Move another digit left. Multiply that digit by 162 (256) and store that product.
  4. Continue multiplying each incremental digit of the hex value by increasing powers of 16 (4096, 65536, 1048576, …), and remember each product.
  5. Once you’ve multiplied each digit of the hex value by the proper power of 16, add them all up. That sum is the decimal equivalent of your hex value.

Hex-to-Decimal Example: Convert 0xC0DE

Here’s an example of a four-digit hexadecimal value, 0xC0DE, that we want to convert to decimal. Creating a table and sorting the digits into separate columns can make the conversion process easier:

Hexadecimal Digit Notes
Digit Positions (n) 3 2 1 0 These values are statically assigned, they grow to the left.
Hex Digits Sorted C 0 D E This part’s easy, plug your hex values in from right-to-left.
Convert A-F 12 0 13 14 Convert hex values A-F to 10-15.
Multiply by 16n 12 × 163 0 × 162 13 × 161 14 × 160 The exponent of 16 is the position, n.
Resulting Products 49152 0 208 14 The product of hex digit and the power of 16.
Sum Up All Products 49374 Our decimal equivalent!

 

There you have it. CODE16 = 4937410!

This table method is perfect for keeping all of your hex digits, positions, and powers-of-16 in line. To convert larger hex numbers, just add a columns to the left and increase n.

Now that you know how to do it by hand, save yourself a little time and use a calculator.

The Western Design Center, Inc. - 2023