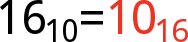This page covers the very basics of hex, including an overview of the digits we use to represent hex numbers and tools we use to indicate a number is a hex value. We also cover very simple “decimal-to-hex” conversion in the form of hexadecimal counting.
The Digits: 0-9 and A-F
Hexadecimal is a base-16 number system. That means there are 16 possible digits used to represent numbers. 10 of the numerical values you’re probably used to seeing in decimal numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9; those values still represent the same value you’re used to. The remaining six digits are represented by A, B, C, D, E, and F, which map out to values of 10, 11, 12, 13, 14, and 15.
You’ll probably encounter both upper and lower case representations of A-F. Both work. There isn’t much of a standard in terms of upper versus lower case. A3F is the same number as a3f is the same number as A3f.
Subscripts
Decimal and hexadecimal have 10 digits in common, so they can create a lot of similar-looking numbers. But 10 in hex is a wholly different number from that in decimal. In fact hex 10 is equivalent to decimal 16. We need a way to explicitly state whether a number we’re talking about is base 10 or base 16 (or base 8, or base 2). Enter base subscripts:
Hexadecimal 10, indicated by a subscript 16, is equivalent to decimal 16 (notice the subscript 10).
As you’ll see further down, subscripts aren’t the only way to explicitly state the base of a number. Subscripts are just the most literal system we can use.
Counting in Hex
Counting in hex is a lot like counting in decimal, except there are six more digits to deal with. Once a digit place becomes greater than “F”, you roll that place over to “0”, and increment the digit to the left by 1.
Let’s do some counting:
| Decimal | Hexadecimal | … | Decimal | Hexadecimal |
|---|---|---|---|---|
| 0 | 0 | 8 | 8 | |
| 1 | 1 | 9 | 9 | |
| 2 | 2 | 10 | A | |
| 3 | 3 | 11 | B | |
| 4 | 4 | 12 | C | |
| 5 | 5 | 13 | D | |
| 6 | 6 | 14 | E | |
| 7 | 7 | 15 | F |
Once you’ve reached F16, just as you would roll from 910 to 1010 in decimal, you roll up to 1016:
| Decimal | Hexadecimal | … | Decimal | Hexadecimal |
|---|---|---|---|---|
| 16 | 10 | 24 | 18 | |
| 17 | 11 | 25 | 19 | |
| 18 | 12 | 26 | 1A | |
| 19 | 13 | 27 | 1B | |
| 20 | 14 | 28 | 1C | |
| 21 | 15 | 29 | 1D | |
| 22 | 16 | 30 | 1E | |
| 23 | 17 | 31 | 1F |
And once you’ve reached 1F16, roll up to 2016 and keep churning the right-most digit from 0 to F.
Hex Identifiers
“BEEF, it’s what’s for dinner”. Am I channelling my inner Sam Elliott (McConaughey?), or expressing my hunger for the decimal number 48879? To avoid confusing situations like that, you’ll usually see a hexadecimal number prefixed (or suffixed) with one of these identifiers:
| Identifier | Example | Notes |
|---|---|---|
| 0x | 0x47DE | This prefix shows up a lot in UNIX and C-based programming languages (like Arduino!). |
| # | #FF7734 | Color references in HTML and image editting programs. |
| % | %20 | Often used in URLs to express characters like “Space” (%20). |
| \x | \x0A | Often used to express character control codes like “Backspace” (\x08), “Escape” (\x1B), and “Line Feed” (\x0A). |
| &#x | Ω | Used in HTML, XML, and XHTML to express unicode characters (e.g. Ω prints an Ω). |
| 0h | 0h5E | A prefix used by many programmable graphic calculators (e.g. TI-89). |
| Numeral/Text Subscript | BE3716, 13Fhex | This is more of a mathematical represenatation of base 16 numbers. Decimal numbers can be represented with a subscript 10 (base 10). Binary is base 2. |
There are a variety of other prefixes and suffixes that are specific to certain programming languages. Assembly languagues, for example, might use an “H” or “h” suffix (e.g. 7Fh) or a “$” prefix ($6AD). Consult examples if you’re not sure which prefix or suffix to use with your programming language.
In summary: DECAF? A horrible abomination of coffee. 0xDECAF? A perfectly acceptable, 5-digit hexadecimal number.